Newton Solver Benchmark Set - Spiegelman et at. (2016)

The files in this directory can be used to recreate the figures from Fraters et al. [2019] reproducing the Spiegelman et al. [2016] benchmark. input.prm is the setup of one of the benchmark models and run.sh will execute a series of model runs. Before you can execute the benchmark you will have to compile the plugin drucker_prager_compositions.cc in the same directory, the process of compiling plugins is described in Running benchmarks that require code. After you have executed run.sh, you can use the gnuplot plotting script plot.gnuplot to recreate Fig. 4 of Fraters et al. [2019].

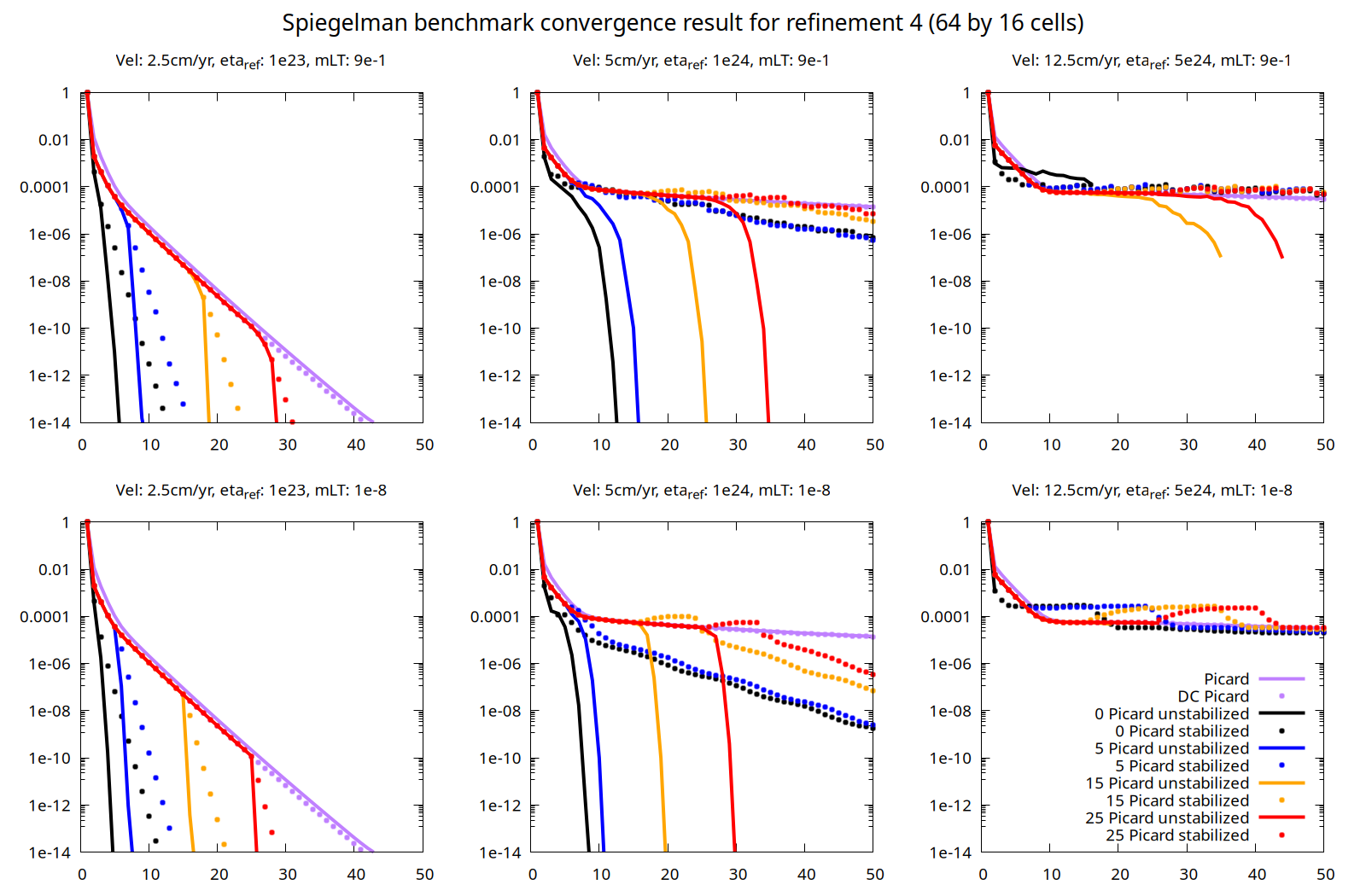
Fig. 290 Convergence history of several models of the Spiegelman et al. benchmark: a reproduction of three of the nine pressure dependent Drucker–Prager cases with a resolution of 64 × 16 cells. Top: results for computations where linear systems are solved with a maximum relative tolerance of 0.9. Bottom: The same models solved with a tolerance of \(10^{-8}\). The initial Picard iteration is always solved to a linear tolerance of \(10^{-14}\). Left to right: different prescribed velocities of u0 = 2.5, 5, and 12.5 cm\yr, and different background reference viscosities of respectively \(\eta_{ref}\) = \(10^{23}\), \(10^{24}\) and \(10^{25}\) Pa s. Horizontal axis: number of the non-linear (outer) iteration; and vertical axis: non-linear residual. “DC Picard” refers to a defect correction Picard iteration, see the paper describing this solver.

The nonlinear convergence behavior of ASPECT’s different nonlinear solvers is shown in Fig. 290.